Thursday, 31 March 2016

class 12 Notes for Electrostatics (Part 2)

Electric field


Electric field lines are useful for visualizing the electric field. Field lines begin on positive charge and terminate on negative charge. Electric field lines are parallel to the direction of the electric field, and the density of these field lines is a measure of the magnitude of the electric field at any given point. The electric field, \vec{E}, (in units of voltsper meter) is a vector field that can be defined everywhere, except at the location of point charges (where it diverges to infinity). It is convenient to place a hypothetical test charge at a point (where no charges are present). By Coulomb's Law, this test charge will experience a force that can be used to define the electric field as follow
\vec{F} = q \vec{E}.\,
(See the Lorentz equation if the charge is not stationary.)
Consider a collection of N particles of charge Q_i, located at points \vec r_i (called source points), the electric field at \vec r  (called the field point) is:
\vec{E}(\vec r) =\frac{1}{4\pi \varepsilon _0}\sum_{i=1}^N \frac{\widehat\mathcal R_i Q_i}{\left \|\mathcal\vec R_i \right \|^2} ,
where  \vec\mathcal R_i = \vec r - \vec r_i , is the displacement vector from a source point\vec r_i to the field point \vec r , and  \widehat\mathcal R_i = \vec\mathcal R_i / \left \|\vec\mathcal R_i \right \| is a unit vector that indicates the direction of the field. For a single point charge at the origin, the magnitude of this electric field is E =k_eQ/\mathcal R^2, and points away from that charge is positive. That fact that the force (and hence the field) can be calculated by summing over all the contributions due to individual source particles is an example of the superposition principle. The electric field produced by a distribution of charges is given by the volume charge density \rho (\vec r) and can be obtained by converting this sum into a triple integral:
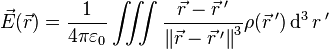
\vec{E}(\vec r)= \frac {1}{4 \pi \varepsilon_0} \iiint \frac {\vec r - \vec r \,'}{\left \| \vec r - \vec r \,' \right \|^3} \rho (\vec r \,')\operatorname{d}^3 r\,'
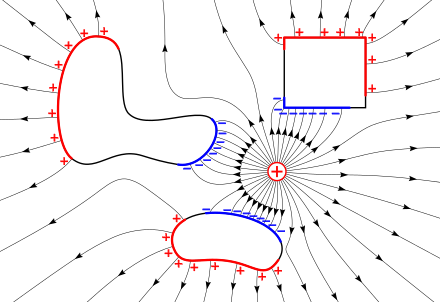
The electrostatic field (lines with arrows) of a nearby positive charge (+)causes the mobile charges in conductive objects to separate due to electrostatic induction. Negative charges (blue) are attracted and move to the surface of the object facing the external charge. Positive charges (red) are repelled and move to the surface facing away. These induced surface charges are exactly the right size and shape so their opposing electric field cancels the electric field of the external charge throughout the interior of the metal. Therefore the electrostatic field everywhere inside a conductive object is zero, and the electrostatic potential is constant.

Gauss's law[edit]

Gauss's law states that " the total electric flux through any closed surface in free space of any shape drawn in an electric field is proportional to the total electric charge enclosed by the surface." Mathematically, Gauss's law takes the form of an integral equation:
\oint_S\vec{E} \cdot\mathrm{d}\vec{A} = \frac{1}{\varepsilon_0}\,Q_{enclosed}=\int_V{\rho\over\varepsilon_0}\cdot\operatorname{d}^3 r,
where  \operatorname{d}^3 r =\mathrm{d}x \ \mathrm{d}y \ \mathrm{d}z  is a volume element. If the charge is distributed over a surface or along a line, replace  \rho\mathrm{d}^3r  by  \sigma\mathrm{d}A  or  \lambda\mathrm{d}\ell . The Divergence Theorem allows Gauss's Law to be written in differential form:
\vec{\nabla}\cdot\vec{E} = {\rho\over\varepsilon_0}.
where \vec{\nabla} \cdot is the divergence operator.

Poisson and Laplace equations[edit]

The definition of electrostatic potential, combined with the differential form of Gauss's law (above), provides a relationship between the potential Φ and the charge density ρ:
{\nabla}^2 \phi = - {\rho\over\varepsilon_0}.
This relationship is a form of Poisson's equation. In the absence of unpaired electric charge, the equation becomes Laplace's equation:
{\nabla}^2 \phi = 0,

now rest continue in part 3.
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)