An electric potential (also called the electric field potential or the electrostatic potential) is the amount of electric potential energy that a unitary point electric charge would have if located at any point in space, and is equal to the work done by an external agent in carrying a unit of positive charge from infinity to that point without any acceleration.
According to theoretical electromagnetics, electric potential is a scalar quantity denoted by V, equal to the electric potential energy of any charged particle at any location (measured in joules) divided by the charge of that particle (measured in coulombs). By dividing out the charge on the particle a remainder is obtained that is a property of the electric field itself.
This value can be calculated in either a static (time-invariant) or a dynamic (varying with time)electric field at a specific time in units of joules per coulomb (J C−1), or volts (V). The electric potential at infinity is assumed to be zero.
A generalized electric scalar potential is also used in electrodynamics when time-varying electromagnetic fields are present, but this can not be so simply calculated. The electric potential and the magnetic vector potential together form a four vector, so that the two kinds of potential are mixed under Lorentz transformations.
Introduction[edit]
Classical mechanics explores concepts such as force, energy, potential etc. Force and potential energy are directly related. A net force acting on any object will cause it to accelerate. As an object moves in the direction in which the force accelerates it, its potential energy decreases: the gravitational potential energy of a cannonball at the top of a hill is greater than at the base of the hill. As it rolls downhill its potential energy decreases, being translated to motion, inertial (kinetic) energy.
It is possible to define the potential of certain force fields so that the potential energy of an object in that field depends only on the position of the object with respect to the field. Two such force fields are the gravitational field and an electric field (in the absence of time-varying magnetic fields). Such fields must affect objects due to the intrinsic properties of the object (e.g., mass or charge) and the position of the object.
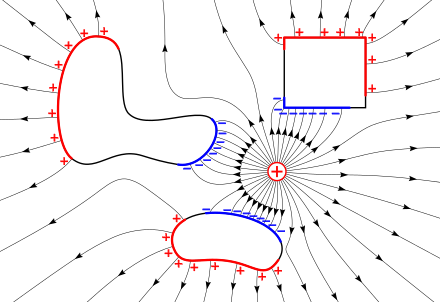
Objects may possess a property known as electric charge and an electric field exerts a force on charged objects. If the charged object has a positive charge the force will be in the direction of the electric field vector at that point while if the charge is negative the force will be in the opposite direction. The magnitude of the force is given by the quantity of the charge multiplied by the magnitude of the electric field vector.
Electrostatics[edit]
Main article: Electrostatics
The electric potential at a point r in a static electric field E is given by the line integral
where C is an arbitrary path connecting the point with zero potential to r. When the curl ∇ × E is zero, the line integral above does not depend on the specific path C chosen but only on its endpoints. In this case, the electric field is conservative and determined by the gradient of the potential:
Then, by Gauss's law, the potential satisfies Poisson's equation:
The concept of electric potential is closely linked with potential energy. A test charge q has an electric potential energy UE given by
The potential energy and hence also the electric potential is only defined up to an additive constant: one must arbitrarily choose a position where the potential energy and the electric potential are zero.
These equations cannot be used if the curl ∇ × E ≠ 0, i.e., in the case of a nonconservative electric field (caused by a changing magnetic field; see Maxwell's equations). The generalization of electric potential to this case is described below.
Electric potential due to a point charge[edit]
The electric potential created by a point charge Q, at a distance r from the charge (relative to the potential at infinity), can be shown to be
where ε0 is the electric constant (permittivity of vacuum). This is known as the Coulomb potential.
The electric potential due to a system of point charges is equal to the sum of the point charges' individual potentials. This fact simplifies calculations significantly, since addition of potential (scalar) fields is much easier than addition of the electric (vector) fields.
The equation given above for the electric potential (and all the equations used here) are in the forms required by SI units. In some other (less common) systems of units, such as CGS-Gaussian, many of these equations would be altered.
Generalization to electrodynamics[edit]
When time-varying magnetic fields are present (which is true whenever there are time-varying electric fields and vice versa), it is not possible to describe the electric field simply in terms of a scalar potential V because the electric field is no longer conservative:  is path-dependent because
is path-dependent because  (Faraday's law of induction).
(Faraday's law of induction).
 is path-dependent because
is path-dependent because  (Faraday's law of induction).
(Faraday's law of induction).
Instead, one can still define a scalar potential by also including the magnetic vector potential A. In particular, A is defined to satisfy:
where B is the magnetic field. Because the divergence of the magnetic field is always zero due to the absence of magnetic monopoles, such anA can always be found. Given this, the quantity
is a conservative field by Faraday's law and one can therefore write
where V is the scalar potential defined by the conservative field F.
The electrostatic potential is simply the special case of this definition where A is time-invariant. On the other hand, for time-varying fields,
unlike electrostatics.
Units[edit]
The SI unit of electric potential is the volt (in honor of Alessandro Volta), which is why a difference in electric potential between two points is known as voltage. Older units are rarely used today. Variants of the centimeter gram second system of units included a number of different units for electric potential, including the abvolt and the statvolt.
Galvani potential versus electrochemical potential[edit]
Inside metals (and other solids and liquids), the energy of an electron is affected not only by the electric potential, but also by the specific atomic environment that it is in. When a voltmeter is connected between two different types of metal, it measures not the electric potential difference, but instead the potential difference corrected for the different atomic environments.[1] The quantity measured by a voltmeter is calledelectrochemical potential or fermi level, while the pure unadjusted electric potential is sometimes called Galvani potential. The terms "voltage" and "electric potential" are a bit ambiguous in that, in practice, they can refer to either of these in different contexts.
thanks for reading




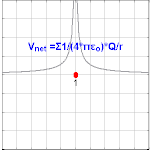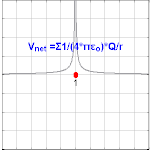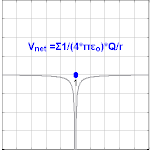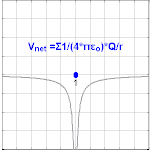








 , called the
, called the  , points from regions of high electric potential to regions of low electric potential, expressed mathematically as
, points from regions of high electric potential to regions of low electric potential, expressed mathematically as
 to point
to point  is the following
is the following 
 , can be calculated from a
, can be calculated from a  . We integrate from a point at infinity, and assume a collection of
. We integrate from a point at infinity, and assume a collection of  particles of charge
particles of charge  , are already situated at the points
, are already situated at the points  . This potential energy (in
. This potential energy (in 
 is the distance of each charge
is the distance of each charge  from the
from the  , which situated at the point
, which situated at the point  , and
, and  is the electric potential that would be at
is the electric potential that would be at  . The total
. The total 

 is what would be measured at
is what would be measured at  :
: ,
, and
and  ; they yield equal values for the total electrostatic energy only if both are integrated over all space.
; they yield equal values for the total electrostatic energy only if both are integrated over all space. ,
, , (in units of
, (in units of 

 is the displacement vector from a source point
is the displacement vector from a source point is a
is a  and points away from that charge is positive. That fact that the force (and hence the field) can be calculated by summing over all the contributions due to individual source particles is an example of the
and points away from that charge is positive. That fact that the force (and hence the field) can be calculated by summing over all the contributions due to individual source particles is an example of the  and can be obtained by converting this sum into a
and can be obtained by converting this sum into a 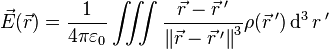

 is a volume element. If the charge is distributed over a surface or along a line, replace
is a volume element. If the charge is distributed over a surface or along a line, replace  by
by  or
or  . The
. The 
 is the
is the 
