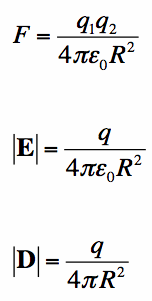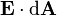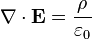Gauss' Law
Gauss' Law is the first of Maxwell's Equations which dictates how the Electric Field behaves around electric charges. Gauss' Law can be written in terms of the Electric Flux Density and the Electric Charge Density as:
In Equation [1], the symbol
 is the divergence operator.
Equation [1] is known as Gauss' Law in point form. That is, Equation [1] is true at any point in space. That is, if there exists electric charge somewhere, then the divergence of D at that point is nonzero, otherwise it is equal to zero.
To get some more intuition on Gauss' Law, let's look at Gauss' Law in integral form. To do this, we assume some arbitrary volume (we'll call it V) which has a boundary (which is written S). Then integrating Equation [1] over the volume V gives Gauss' Law in integral form:
I probably made things less clear, but let's go through it real quick. As an example, look at Figure 1. We have a volume V, which is the cube. The surface S is the boundary of the cube (i.e. the 6 flat faces that form the boundary of the volume).
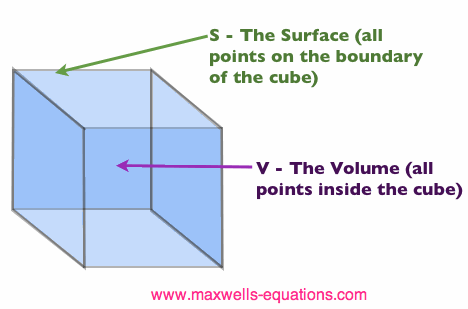 Figure 1. Illustration of a volume V with boundary surface S.
Equation [2] states that the amount of charge inside a volume V (=
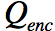 ) is equal to the total amount of Electric Flux (D) exiting the surface S. That is, to determine the Electric Flux leaving the region V, we only need to know how much electric charge is within the volume. We rewrite Equation [2] with more of the terms defined in Equation [3]:
An example with the cube in Figure 1 might help make this clear. Look at the point P in Figure 2, where we have drawn the D field vector:
 Figure 2. The D Field on the Surface Can be Broken Down into Tangential (Dt) and Normal (Dn) Components.
We can rewrite any field in terms of its tangential and normal components, as shown in Figure 2. From Equation [3], we are only interested in the component of D normal (orthogonal or perpendicular) to the surface S. We write this as Dn. The tangential component Dt flows along the surface. If you imagine the D field as a water flow, then only the component Dn would contribute to water actually leaving the volume - Dt is just water flowing around the surface.
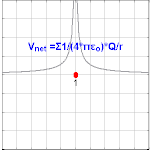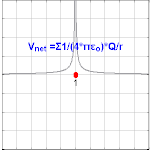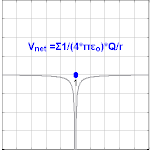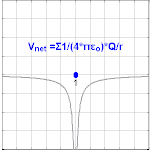
Hence, Gauss' law is a mathematical statement that the total Electric Flux exiting any volume is equal to the total charge inside. Hence, if the volume in question has no charge within it, the net flow of Electric Flux out of that region is zero. If there is positive charge within a volume, then there exists a positive amount of Electric Flux exiting any volume that surrounds the charge. If there is negative charge within a volume, then there exists a negative amount of Electric Flux exiting (i.e. the Electric Flux enters the volume).
Interpretation of Gauss' Law
What does this matter? Gauss' Law states that electric charge acts as sources or sinks for Electric Fields.
If you use the water analogy again, positive charge gives rise to flow out of a volume - this means positive electric charge is like a source (a faucet - pumping water into a region). Conversely, negative charge gives rise to flow into a volume - this means negative charge acts like a sink (fields flow into a region and terminate on the charge).
This gives us a lot of intuition about the way fields can physically act in any scenario. For instance, here are possible and impossible situations for the Electric Field, as decided by the universe in the Law of Gauss it setup:
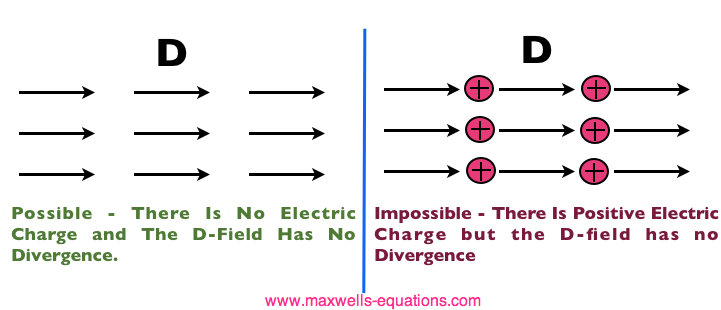 Figure 3. Example #1 of Gauss' Law: The D Field Must Have the Correct Divergence. Figure 4. Example #2 of Gauss' Law: The Charges Dictate the Divergence of D . Figure 5. Example #3 of Gauss' Law: Negative Charge Indicates the Divergence of D should be negative.
If you observe the way the D field must behave around charge, you may notice that Gauss' Law then is equivalent to the Force Equation for charges, which gives rise to the E field equation for point charges:
Equation [4] shows that charges exert a force on them, which means there exists E-fields that are away from positive charge and towards negative charge. This means opposite charges attract and negative charges repel. And since D and E are related by permittivity, we see that Gauss' Law is a more formal statement of the force equation for electric charges.
In summary, Gauss' Law means the following is true:
And there you go! If you understand the above statements you understand Gauss' Law, probably better than the mathematicians who invent super complicated math to explain physical phenomena! Intuition trumps complication, always.
|
Friday, 1 April 2016
Maxwell's Equations Gauss's law
Gauss's law
This article is about Gauss's law concerning the electric field. For analogous law concerning different fields, see Gauss's law for magnetismand Gauss's law for gravity. For Gauss's theorem, a mathematical theorem relevant to all of these laws, see Divergence theorem.
| Electromagnetism |
|---|
 |
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution ofelectric charge to the resulting electric field.
The law was formulated by Carl Friedrich Gauss in 1835, but was not published until 1867.[1] It is one of Maxwell's four equations, which form the basis of classical electrodynamics, the other three being Gauss's law for magnetism, Faraday's law of induction, and Ampère's law with Maxwell's correction. Gauss's law can be used to derive Coulomb's law, and vice versa.
Qualitative description
In words, Gauss's law states that:
- The net electric flux through any closed surface is equal to 1⁄ε times the net electric charge within that closed surface.[3]
Gauss's law has a close mathematical similarity with a number of laws in other areas of physics, such as Gauss's law for magnetism andGauss's law for gravity. In fact, any "inverse-square law" can be formulated in a way similar to Gauss's law: For example, Gauss's law itself is essentially equivalent to the inverse-square Coulomb's law, and Gauss's law for gravity is essentially equivalent to the inverse-square Newton's law of gravity.
Gauss's law is something of an electrical analogue of Ampère's law, which deals with magnetism.
The law can be expressed mathematically using vector calculus in integral form and differential form, both are equivalent since they are related by the divergence theorem, also called Gauss's theorem. Each of these forms in turn can also be expressed two ways: In terms of a relation between the electric field E and the total electric charge, or in terms of the electric displacement field D and the free electric charge.[4]
Equation involving E field
Gauss's law can be stated using either the electric field E or the electric displacement field D. This section shows some of the forms with E; the form with D is below, as are other forms with E.
Integral form
Gauss's law may be expressed as:[5]
where ΦE is the electric flux through a closed surface S enclosing any volume V, Q is the total charge enclosed within S, and ε0 is the electric constant. The electric flux ΦE is defined as a surface integral of the electric field:
where E is the electric field, dA is a vector representing an infinitesimal element of area of the surface,[note 1] and · represents the dot product of two vectors.
Since the flux is defined as an integral of the electric field, this expression of Gauss's law is called the integral form.
Applying the integral form
Main article: Gaussian surface
See also Capacitance (Gauss's law)
If the electric field is known everywhere, Gauss's law makes it quite easy, in principle, to find the distribution of electric charge: The charge in any given region can be deduced by integrating the electric field to find the flux.
However, much more often, it is the reverse problem that needs to be solved: The electric charge distribution is known, and the electric field needs to be computed. This is much more difficult, since if you know the total flux through a given surface, that gives almost no information about the electric field, which (for all you know) could go in and out of the surface in arbitrarily complicated patterns.
An exception is if there is some symmetry in the situation, which mandates that the electric field passes through the surface in a uniform way. Then, if the total flux is known, the field itself can be deduced at every point. Common examples of symmetries which lend themselves to Gauss's law include cylindrical symmetry, planar symmetry, and spherical symmetry. See the article Gaussian surface for examples where these symmetries are exploited to compute electric fields.
Differential form
By the divergence theorem, Gauss's law can alternatively be written in the differential form:
where ∇ · E is the divergence of the electric field, ε0 is the electric constant, and ρ is the total electric charge density (charge per unit volume).
Equivalence of integral and differential forms
Main article: Divergence theorem
The integral and differential forms are mathematically equivalent, by the divergence theorem. Here is the argument more specifically.
[show]Outline of proof
Equation involving D field
See also: Maxwell's equations
Free, bound, and total charge
Main article: Electric polarization
The electric charge that arises in the simplest textbook situations would be classified as "free charge"—for example, the charge which is transferred in static electricity, or the charge on a capacitor plate. In contrast, "bound charge" arises only in the context of dielectric (polarizable) materials. (All materials are polarizable to some extent.) When such materials are placed in an external electric field, the electrons remain bound to their respective atoms, but shift a microscopic distance in response to the field, so that they're more on one side of the atom than the other. All these microscopic displacements add up to give a macroscopic net charge distribution, and this constitutes the "bound charge".
Although microscopically, all charge is fundamentally the same, there are often practical reasons for wanting to treat bound charge differently from free charge. The result is that the more "fundamental" Gauss's law, in terms of E (above), is sometimes put into the equivalent form below, which is in terms of D and the free charge only.
Integral form
This formulation of Gauss's law states the total charge form:
where ΦD is the D-field flux through a surface S which encloses a volume V, and Qfree is the free charge contained in V. The flux ΦD is defined analogously to the flux ΦE of the electric field E through S:
Differential form
The differential form of Gauss's law, involving free charge only, states:
where ∇ · D is the divergence of the electric displacement field, and ρfree is the free electric charge density.
Equivalence of total and free charge statements
[show]Proof that the formulations of Gauss's law in terms of free charge are equivalent to the formulations involving total charge.
Equation for linear materials[edit]
In homogeneous, isotropic, nondispersive, linear materials, there is a simple relationship between E and D:
where ε is the permittivity of the material. For the case of vacuum (aka free space), ε = ε0. Under these circumstances, Gauss's law modifies to
for the integral form, and
for the differential form.
Relation to Coulomb's law
Deriving Gauss's law from Coulomb's law
Gauss's law can be derived from Coulomb's law.
[show]Outline of proof
Note that since Coulomb's law only applies to stationary charges, there is no reason to expect Gauss's law to hold for moving charges based on this derivation alone. In fact, Gauss's law does hold for moving charges, and in this respect Gauss's law is more general than Coulomb's law.
Deriving Coulomb's law from Gauss's law
Strictly speaking, Coulomb's law cannot be derived from Gauss's law alone, since Gauss's law does not give any information regarding the curlof E (see Helmholtz decomposition and Faraday's law). However, Coulomb's law can be proven from Gauss's law if it is assumed, in addition, that the electric field from a point charge is spherically-symmetric (this assumption, like Coulomb's law itself, is exactly true if the charge is stationary, and approximately true if the charge is in motion).
Thanks for reading
Thursday, 31 March 2016
class 12 Notes for Electric potential
An electric potential (also called the electric field potential or the electrostatic potential) is the amount of electric potential energy that a unitary point electric charge would have if located at any point in space, and is equal to the work done by an external agent in carrying a unit of positive charge from infinity to that point without any acceleration.
According to theoretical electromagnetics, electric potential is a scalar quantity denoted by V, equal to the electric potential energy of any charged particle at any location (measured in joules) divided by the charge of that particle (measured in coulombs). By dividing out the charge on the particle a remainder is obtained that is a property of the electric field itself.
This value can be calculated in either a static (time-invariant) or a dynamic (varying with time)electric field at a specific time in units of joules per coulomb (J C−1), or volts (V). The electric potential at infinity is assumed to be zero.
A generalized electric scalar potential is also used in electrodynamics when time-varying electromagnetic fields are present, but this can not be so simply calculated. The electric potential and the magnetic vector potential together form a four vector, so that the two kinds of potential are mixed under Lorentz transformations.
Introduction[edit]
Classical mechanics explores concepts such as force, energy, potential etc. Force and potential energy are directly related. A net force acting on any object will cause it to accelerate. As an object moves in the direction in which the force accelerates it, its potential energy decreases: the gravitational potential energy of a cannonball at the top of a hill is greater than at the base of the hill. As it rolls downhill its potential energy decreases, being translated to motion, inertial (kinetic) energy.
It is possible to define the potential of certain force fields so that the potential energy of an object in that field depends only on the position of the object with respect to the field. Two such force fields are the gravitational field and an electric field (in the absence of time-varying magnetic fields). Such fields must affect objects due to the intrinsic properties of the object (e.g., mass or charge) and the position of the object.
Objects may possess a property known as electric charge and an electric field exerts a force on charged objects. If the charged object has a positive charge the force will be in the direction of the electric field vector at that point while if the charge is negative the force will be in the opposite direction. The magnitude of the force is given by the quantity of the charge multiplied by the magnitude of the electric field vector.
Electrostatics[edit]
Main article: Electrostatics
The electric potential at a point r in a static electric field E is given by the line integral
where C is an arbitrary path connecting the point with zero potential to r. When the curl ∇ × E is zero, the line integral above does not depend on the specific path C chosen but only on its endpoints. In this case, the electric field is conservative and determined by the gradient of the potential:
Then, by Gauss's law, the potential satisfies Poisson's equation:
The concept of electric potential is closely linked with potential energy. A test charge q has an electric potential energy UE given by
The potential energy and hence also the electric potential is only defined up to an additive constant: one must arbitrarily choose a position where the potential energy and the electric potential are zero.
These equations cannot be used if the curl ∇ × E ≠ 0, i.e., in the case of a nonconservative electric field (caused by a changing magnetic field; see Maxwell's equations). The generalization of electric potential to this case is described below.
Electric potential due to a point charge[edit]
The electric potential created by a point charge Q, at a distance r from the charge (relative to the potential at infinity), can be shown to be
where ε0 is the electric constant (permittivity of vacuum). This is known as the Coulomb potential.
The electric potential due to a system of point charges is equal to the sum of the point charges' individual potentials. This fact simplifies calculations significantly, since addition of potential (scalar) fields is much easier than addition of the electric (vector) fields.
The equation given above for the electric potential (and all the equations used here) are in the forms required by SI units. In some other (less common) systems of units, such as CGS-Gaussian, many of these equations would be altered.
Generalization to electrodynamics[edit]
When time-varying magnetic fields are present (which is true whenever there are time-varying electric fields and vice versa), it is not possible to describe the electric field simply in terms of a scalar potential V because the electric field is no longer conservative: 
is path-dependent because 
(Faraday's law of induction).
is path-dependent because (Faraday's law of induction).
Instead, one can still define a scalar potential by also including the magnetic vector potential A. In particular, A is defined to satisfy:
where B is the magnetic field. Because the divergence of the magnetic field is always zero due to the absence of magnetic monopoles, such anA can always be found. Given this, the quantity
is a conservative field by Faraday's law and one can therefore write
where V is the scalar potential defined by the conservative field F.
The electrostatic potential is simply the special case of this definition where A is time-invariant. On the other hand, for time-varying fields,
unlike electrostatics.
Units[edit]
The SI unit of electric potential is the volt (in honor of Alessandro Volta), which is why a difference in electric potential between two points is known as voltage. Older units are rarely used today. Variants of the centimeter gram second system of units included a number of different units for electric potential, including the abvolt and the statvolt.
Galvani potential versus electrochemical potential[edit]
Inside metals (and other solids and liquids), the energy of an electron is affected not only by the electric potential, but also by the specific atomic environment that it is in. When a voltmeter is connected between two different types of metal, it measures not the electric potential difference, but instead the potential difference corrected for the different atomic environments.[1] The quantity measured by a voltmeter is calledelectrochemical potential or fermi level, while the pure unadjusted electric potential is sometimes called Galvani potential. The terms "voltage" and "electric potential" are a bit ambiguous in that, in practice, they can refer to either of these in different contexts.
thanks for reading
Subscribe to:
Posts (Atom)